Table of Links
1.1 A Polyethylene-based metamaterial for acoustic control
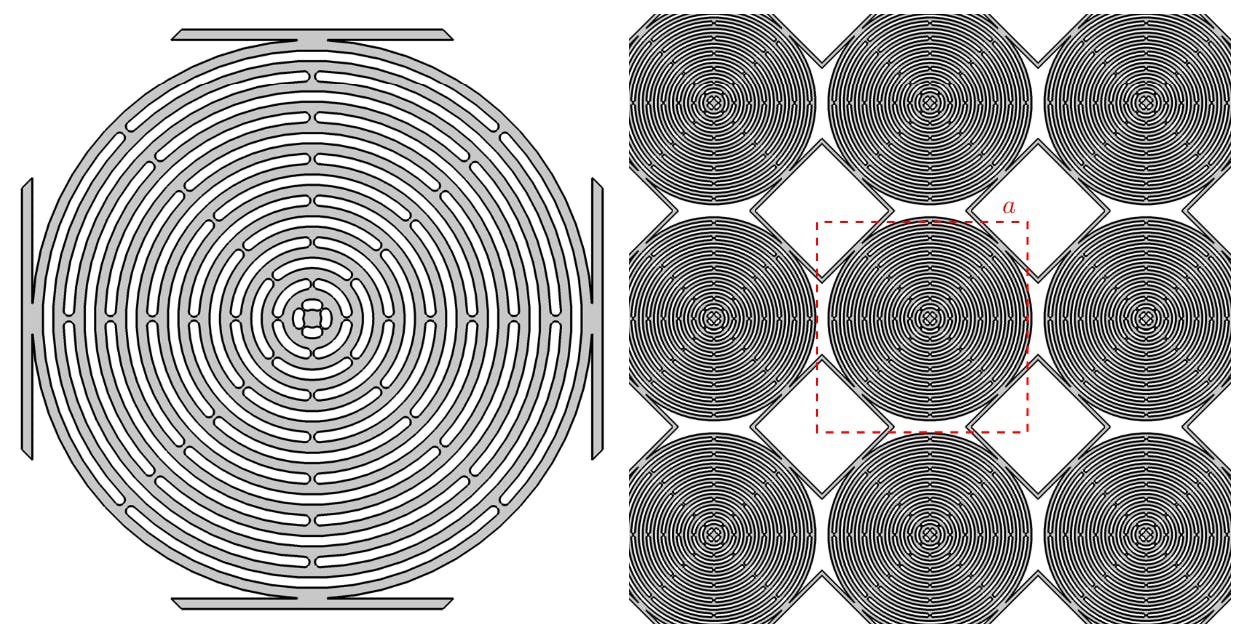
2 Relaxed micromorphic modelling of finite-size metamaterials
2.1 Tetragonal Symmetry / Shape of elastic tensors (in Voigt notation)
4 New considerations on the relaxed micromorphic parameters
4.2 Consistency of the relaxed micromorphic model with respect to a change in the unit cell’s size
4.3 Relaxed micromorphic cut-offs
6 Fitting of the relaxed micromorphic parameters with curvature (with Curl P)
6.1 Asymptotes and 6.2 Fitting
8 Summary of the obtained results
9 Conclusion and perspectives, Acknowledgements, and References
A Most general 4th order tensor belonging to the tetragonal symmetry class
B Coefficients for the dispersion curves without Curl P
C Coefficients for the dispersion curves with P
D Coefficients for the dispersion curves with P◦
2 Relaxed micromorphic modelling of finite-size metamaterials

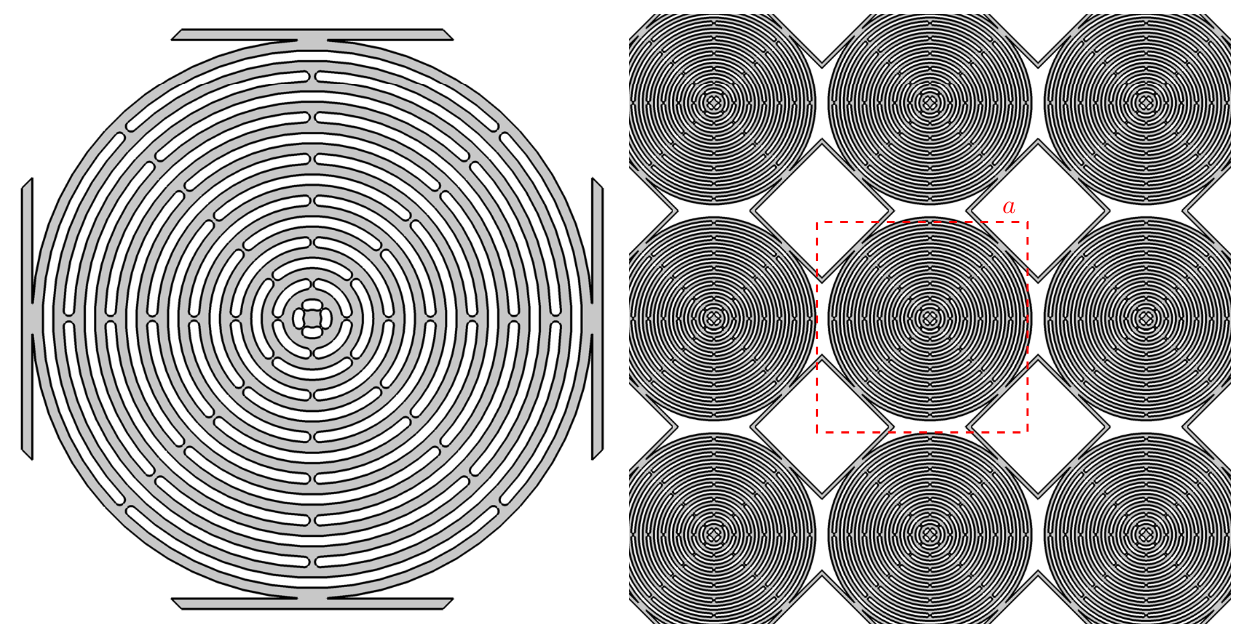

for the classical Cauchy model, and

for the relaxed micromorphic model, where we set
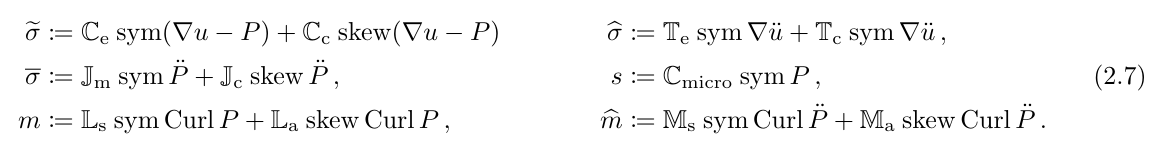
The Neumann boundary condition for the classical Cauchy model are

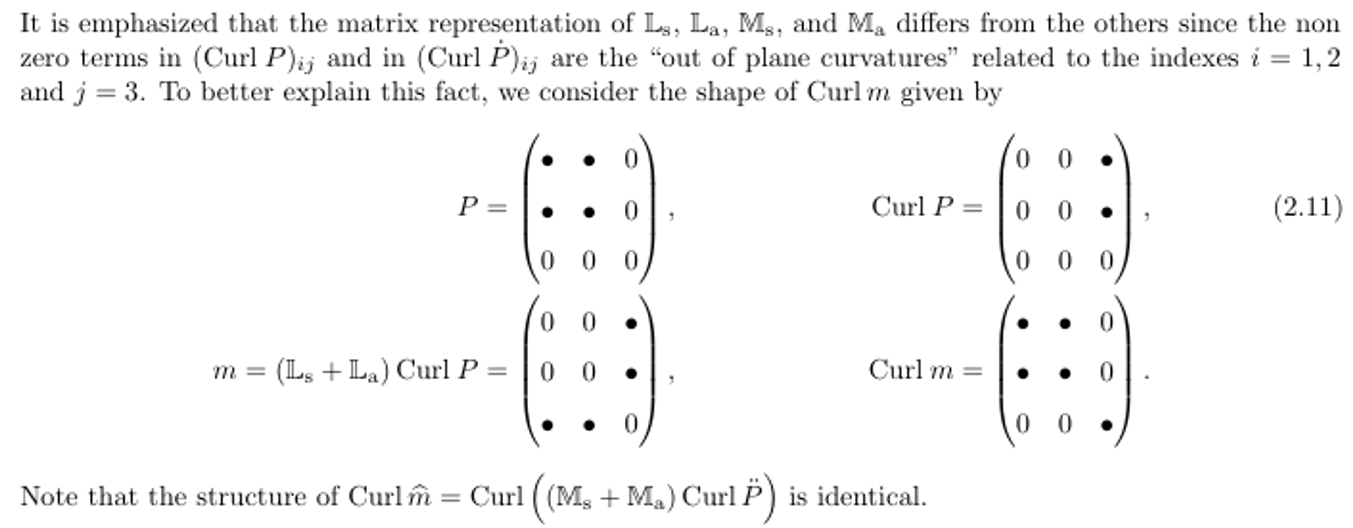
2.1 Tetragonal Symmetry / Shape of elastic tensors (in Voigt notation)


This paper is available on arxiv under CC BY 4.0 DEED license.

[7] We write “m” for “micro” and “M” for “macro” for the corresponding elastic parameters to shorten the following expressions.

Authors:
(1) Jendrik Voss, Institute for Structural Mechanics and Dynamics, Technical University Dortmund and a Corresponding Author ([email protected]);
(2) Gianluca Rizzi, Institute for Structural Mechanics and Dynamics, Technical University Dortmund;
(3) Patrizio Neff, Chair for Nonlinear Analysis and Modeling, Faculty of Mathematics, University of Duisburg-Essen;
(4) Angela Madeo, Institute for Structural Mechanics and Dynamics, Technical University Dortmund.